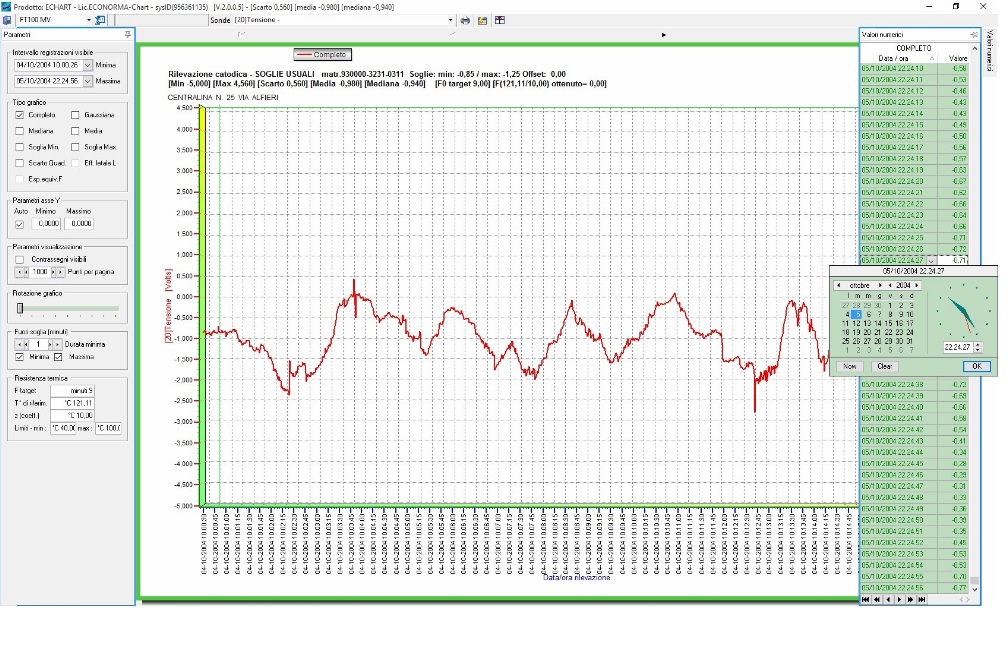
Programma di sviluppo ed elaborazione grafica con selezione dei dati. Si possono graficare e stampare tutti i file relativi alle apparecchiature della ECONORMA S.a.s. serie "FT" . Applicazioni: Istituti di ricerca, Agricoltura, Ecologia, Termotecnica, Laboratori prove, Idrogeologia, ecc. Grafica fino a 131.000 letture con vari modelli matematici. E' disponibile anche il software grafico FT-Chart che sviluppa i grafici provenienti da file Excel e li stampa.
Nome prodotto: FT-Graph-2
Caratteristiche tecniche: Programma di sviluppo ed elaborazione grafica con selezione dei dati.
Categoria Prodotti
PROGRAMMA DI SVILUPPO GRAFICO “FT-Graph-2”
Elaborazione grafica con selezione dei dati. Si possono graficare e stampare tutti i file relativi alle apparecchiature della ECONORMA S.a.s. serie “FT”
Applicazioni: Istituti di ricerca, Industria alimentare (Pastorizzazione-Sterilizzazione) Agricoltura, Ecologia, Termotecnica, Laboratori prove tecnologiche, Idrogeologia, ecc.
… un programma di elaborazione semplice d’uso, potente ed economico !!
INTRODUZIONE
La possibilità di attingere ad una massa notevole di informazioni rischia di impedirci di fatto di utilizzarne anche solo una parte di queste; non basta infatti avere solo l’accesso teorico ad una informazione, ma occorre che essa sia effettivamente fruibile. E’ questo il problema centrale della statistica: rendere davvero utilizzabili grandi quantità di informazioni, teoricamente disponibili, ma di fatto difficilmente gestibili, relative agli oggetti della propria indagine. Infatti, tutte le informazioni, per contribuire effettivamente ad accrescere la conoscenza di un fenomeno, hanno bisogno di essere trattate da vari punti di vista: occorrono tecniche accurate di rilevazione, procedere ad accurate selezioni ed infine un lavoro di organizzazione e di sintesi. Il lavoro statistico ha senso solo se si confronta con grandi quantità di informazioni. Quest’ottica statistica ha guidato il trattamento di sintesi dei dati registrati dai data logger, dati che possono raggiungere la ragguardevole quantità di 131.000. Per rendere disponibili le informazioni rilevate, oltre ovviamente alla possibilità di verificare in dettaglio tutti i valori raccolti, è stata prelevata dalla scienza statistica la modalità di riepilogo dei dati della media.
Lo scopo principale di un valore medio è di fornire un valore numerico capace di rappresentare sinteticamente tutti i dati di un certo insieme. Il software rielabora i valori secondo la media aritmetica e la media mediana.
LA MEDIA ARITMETICA
È la media più conosciuta e applicata, si assume come funzione la somma dei dati. Precisamente si definisce media aritmetica di più numeri quel valore che, sostituito ai dati, lascia invariata la loro somma. La media aritmetica si applica correttamente per determinare il valore centrale di una serie con andamento lineare e anche per avere una misura attendibile di una serie di misure di una grandezza geometrica, fisica. La sua caratteristica è di essere comunque sensibile ai picchi di valore che può assumere l’elenco delle registrazioni, quindi non appiattisce la curva risultante.
LA MEDIANA
Data una successione di dati, disposti in ordine crescente, la mediana è il dato che occupa la posizione centrale. La mediana è una media di posizione e rappresenta il valore centrale della distribuzione quando i dati sono ordinati. Precisamente la mediana non è influenzata dai valori estremi della distribuzione dei valori, quindi se la distribuzione è molto asimmetrica, il valore mediano è più appropriato della media aritmetica per esprimere un valore sintetico delle letture.
RAGGRUPPAMENTO DELLE LETTURE PER VALORE
Il programma dà la possibilità di visualizzare tutte le letture, con data e ora, relative ad un determinato e selezionato valore della misura.
SCARTO QUADRATICO MEDIO – Deviazione Standard
Data una successione di dati ed avendone calcolato la media, lo scarto quadratico medio(sqm) viene utilizzato per dare una valutazione della incertezza da associare a tale stima. Indica quanto la n-esima misura differisce dalla media. Si rivela molto utile per quantificare l’intervallo entro il quale si distribuiscono le varie misure. Si può infatti assumere la deviazione standard come errore da associare al valore medio della misura.
COME SCEGLIERE UNA MEDIA
Un valore sintetico si può calcolare in vari modi. Alcuni valori medi soddisfano a una condizione d’invarianza di un valore globale come la media aritmetica che lascia invariata la somma dei termini. Altri valori medi non considerano tutti i valori della distribuzione, ma solo alcuni di essi, come la mediana, che occupa la posizione centrale della distribuzione. Si usa la media aritmetica per determinare un valore che esprima un concetto di equi distribuzione quando, per esempio, si vuole determinare una media delle temperature. Il valore mediano è il valore centrale della distribuzione e risulta indipendente da forti differenze fra i dati. Non si può dare una regola generale di scelta del tipo di media, ma si deve calcolare più di un valore medio e scegliere quello più interessante per il problema in esame. Le medie cui si ricorre più frequentemente in pratica sono la media aritmetica e la mediana.
VISUALIZZAZIONE GAUSSIANA
Ciò che rende ragguardevole questa distribuzione, è che si tratta di un vero e proprio ponte fra la matematica ed il mondo reale. Supponiamo di effettuare una misurazione, due, tre, …, n volte e di avere uno strumento con un grado di precisione abbastanza elevato. Avremo dei risultati differenti dovuti all’inevitabile imprecisione del nostro strumento e del nostro operato, che sono detti errori accidentali. Se rappresentiamo le misure che otteniamo su un grafico e poi facciamo crescere le misurazioni fino all’infinito, ci accorgeremo che che il grafico si avvicina sempre di più alla curva di Gauss.
Per rimanere sempre aggiornato sulle nostre ultime novità ed offerte.